problem14
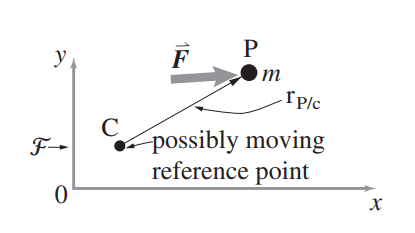
What means “rate of change of angular momentum”? Consider a moving particle P. Consider also a moving point C (moving relative to a Newtonian frame \(\mathcal{F}\) that has an origin 0). For which of these definitions of \(\vec{H}_{/C}\) Is the following equation of motion true (that is, consistent with \(\vec{F} = m \cdot \vec{a}\))? \[\vec{M}_C = \dot{\vec{H}}_{/C}\]
In each case say whether the definition works i) in general, or ii) for some special cases (that you name) concerning the motions of P and C.
- \(\vec{H}_{/C} = \vec{r}_{P/C'} \times \vec{v}_{P/0} m\), where C’ is a point fixed in \(\mathcal{F}\) that instantaneuosly coincides with C.
- \(\vec{H}_{/C} = \vec{r}_{P/C} \times \vec{v}_{P/0} m\).
- \(\vec{H}_{/C} = \vec{r}_{P/C} \times \vec{v}_{P/C} m\).
That is, for each possible definition of \(\vec{H}_{/C}\) you need to calculate \(\dot{\vec{H}}_{C}\) by differentiation and see if and when you get \(\dot{\vec{H}}_{/C} = \vec{r}_{P/C} \times m \vec{a}_{P/\mathcal{F}}\)