problem06

6. Spring and mass (2D). One end of of a negligible-mass spring (k, L0) is pinned to the origin, the other to a mass (m). There is gravity (g). Initial Conditions (ICs): The initial position is \(\vec{r}\_0 = x\_0\hat{i} + y\_0\hat{j}\), and the initial velocity is \(\vec{v}\_0 = v\_{x0}\hat{i} + v\_{y0}\hat{j}\). Motion starts at \(t = 0\) and ends at tend.

(a) Find the Equations of Motion (EoM);  
(b) Assume all parameters and IC’s above are given.  
    i. Plot the trajectory of the mass.  
    ii. Animate the trajectory of the mass.  
(c) How many ways can you think of checking the numerical solution, find as manyas you can, and do the check. The list is started here:
    i. k = 0, all else arbitrary: The motion is parabolic flight (including fallingstraight down as a special case) [Why? The system is then just ballisticsfrom freshman physics];
    ii. x0 = 0, vx0 = 0, all else arbitrary: The motion stays on the y axis [Why?There is no force in the x direction if the mass is on the y axis. Becausethe initial velocity has no x component, the mass never leaves the y axis;
    iii. g = 0,*v0 =*0, all else is arbitrary: The motion stays on a radial line. And,if the motion does not cross the origin, the motion is that of a harmonicoscillator (sinusoidal oscillations, check by plotting, say x vt t. [Why? Writethe EoM and EoMs in polar coordinates⇒ mr¨ = −k(r − L0) ⇒ the harmonic oscillator equation, mr¨∗ =−kr∗, where r∗ ≡ r − L0.
    iv. L0 = 0, all else is arbitrary: ? . [Why? ? .] Hint, this onespecial case is problem 10, below.v. etc.vi. etc.vii. . . .  

Since I already did all of this pretty much in problem 1. I will instead write a simple lorentz system and animate it here.

In file ./lorentz_system.jl:

using DifferentialEquations
using GLMakie

# ----------------------------
# Define the Lorenz System
# ----------------------------
# The Lorenz system is given by:
#   dx/dt = σ (y - x)
#   dy/dt = x (ρ - z) - y
#   dz/dt = x y - β z
function lorenz!(du, u, p, t)
    σ, ρ, β = p
    du[1] = σ * (u[2] - u[1])
    du[2] = u[1] * (ρ - u[3]) - u[2]
    du[3] = u[1] * u[2] - β * u[3]
end

# ----------------------------
# Set Parameters, Initial Conditions, and Solve the ODE
# ----------------------------
# Typical parameter values for the Lorenz system:
p = (10.0, 28.0, 8/3)
u0 = [1.0, 0.0, 0.0]  # initial condition
tspan = (0.0, 40.0)   # simulation time

# Set up the ODE problem and solve it.
prob = ODEProblem(lorenz!, u0, tspan, p)
sol = solve(prob, Tsit5(); saveat=0.01)

# ----------------------------
# Create the Animation with Makie
# ----------------------------
# Create a new scene with a 3D camera.
scene = Scene(resolution = (800, 600), camera = campixel!)

# Plot the full trajectory as a blue line.
lines!(scene, sol[1, :], sol[2, :], sol[3, :],
       color = :blue, linewidth = 1)

# Initialize a red marker for the moving point.
# We start with the first position.
point = scatter!(scene, [sol[1,1]], [sol[2,1]], [sol[3,1]],
                 markersize = 15, color = :red)

# Record the animation. Here, each frame updates the position of the point.
record(scene, "lorenz_animation.gif", length(sol.t)) do i
    # Update the marker position to the i-th solution point.
    point[1].attributes[:positions][] = Point3f0(sol[1,i], sol[2,i], sol[3,i])
    # Optionally, you can adjust the frame rate by pausing briefly:
    sleep(0.001)
end

println("Animation saved as lorenz_animation.gif")

This produces the following animation:

../../media/problem06/lorentz_attractor.gif

The code given on Makie.jl library website:

using GLMakie

Base.@kwdef mutable struct Lorenz
    dt::Float64 = 0.01
    σ::Float64 = 10
    ρ::Float64 = 28
    β::Float64 = 8/3
    x::Float64 = 1
    y::Float64 = 1
    z::Float64 = 1
end

function step!(l::Lorenz)
    dx = l.σ * (l.y - l.x)
    dy = l.x * (l.ρ - l.z) - l.y
    dz = l.x * l.y - l.β * l.z
    l.x += l.dt * dx
    l.y += l.dt * dy
    l.z += l.dt * dz
    Point3f(l.x, l.y, l.z)
end

attractor = Lorenz()

points = Observable(Point3f[])
colors = Observable(Int[])

set_theme!(theme_light())

fig, ax, l = lines(points, color = colors,
    colormap = :inferno, transparency = true,
    axis = (; type = Axis3, protrusions = (0, 0, 0, 0),
              viewmode = :fit, limits = (-30, 30, -30, 30, 0, 50)))

record(fig, "lorenz_makie.gif", 1:120) do frame
    for i in 1:50
        push!(points[], step!(attractor))
        push!(colors[], frame)
    end
    ax.azimuth[] = 1.7pi + 0.3 * sin(2pi * frame / 120)
    notify(points)
    notify(colors)
    l.colorrange = (0, frame)
end

This produces:

../../media/problem06/lorenz_makie.gif

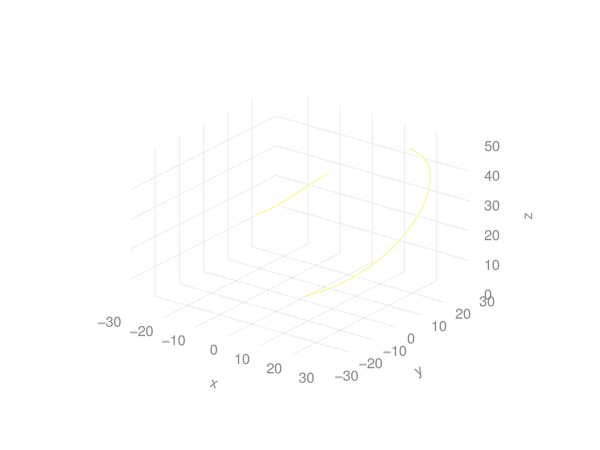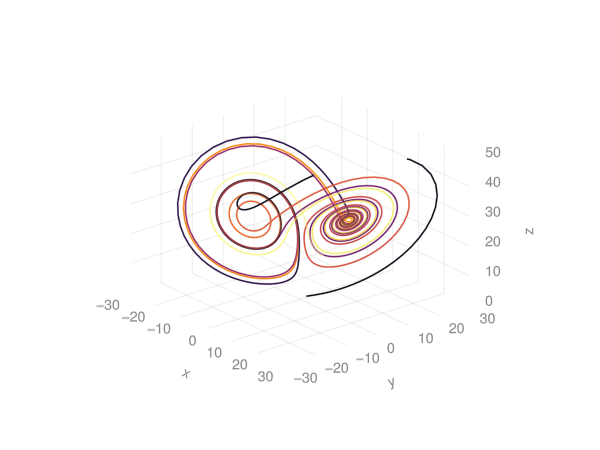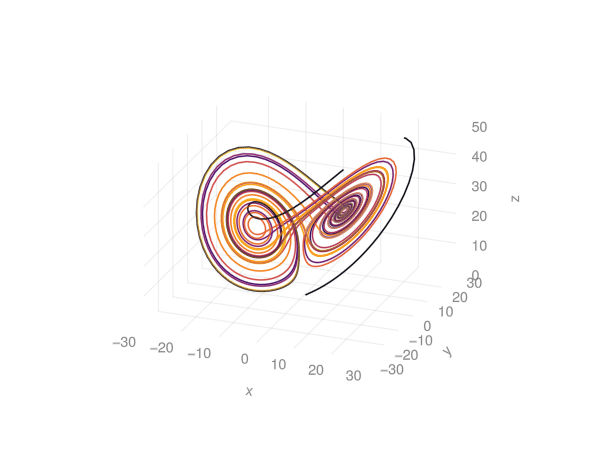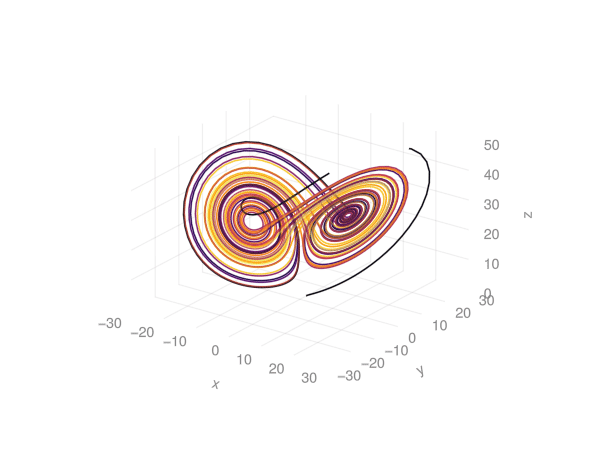
Is there a way to think about verifying lorentz system solutions? I haven’t thought through this yet.